Two sampling methods often applied in practice are: oversampling and undersampling. Oversampling randomly over-samples from the minority class and undersampling randomly down-samples the majority class, both until a threshold is met. Both methods can be seen as a scale in the weight of the loss function, for positive and negative samples, s.t. they’re more equally represented in the likelihood function.

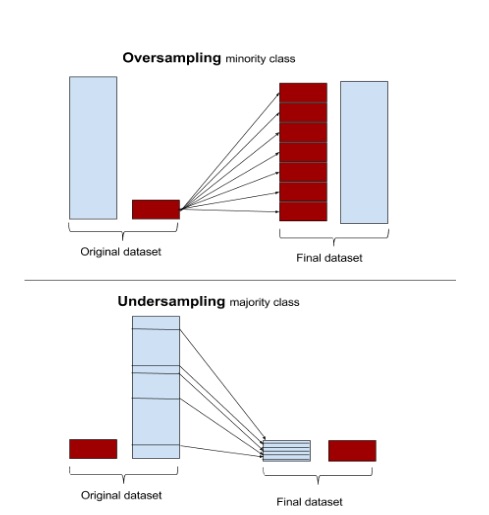
Illustration of under- and over-sampling, taken from [1].

Both methods have downsides. The oversampling method replicates instances of the minority class making it look like this class has lower variance and the undersampling method makes the majority class look like it has higher variance.

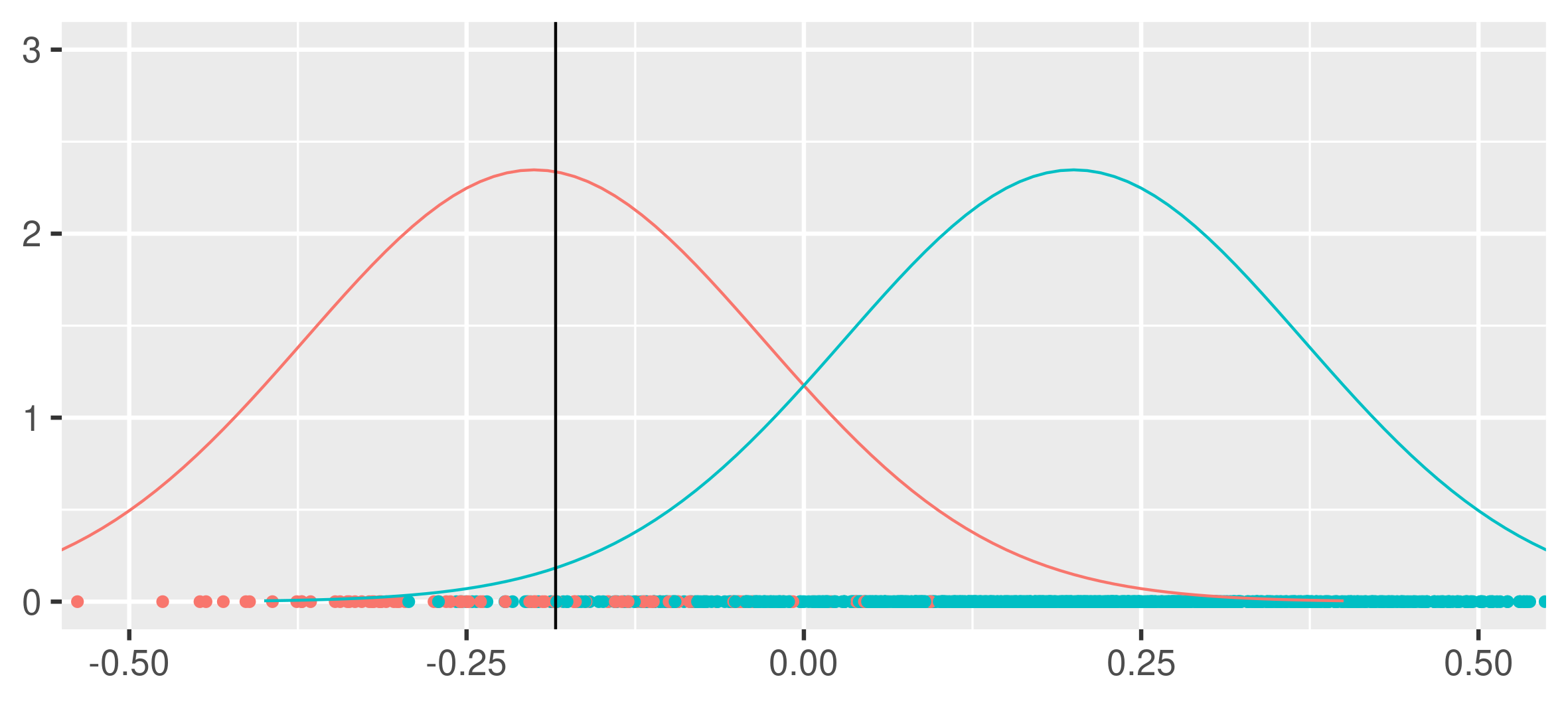
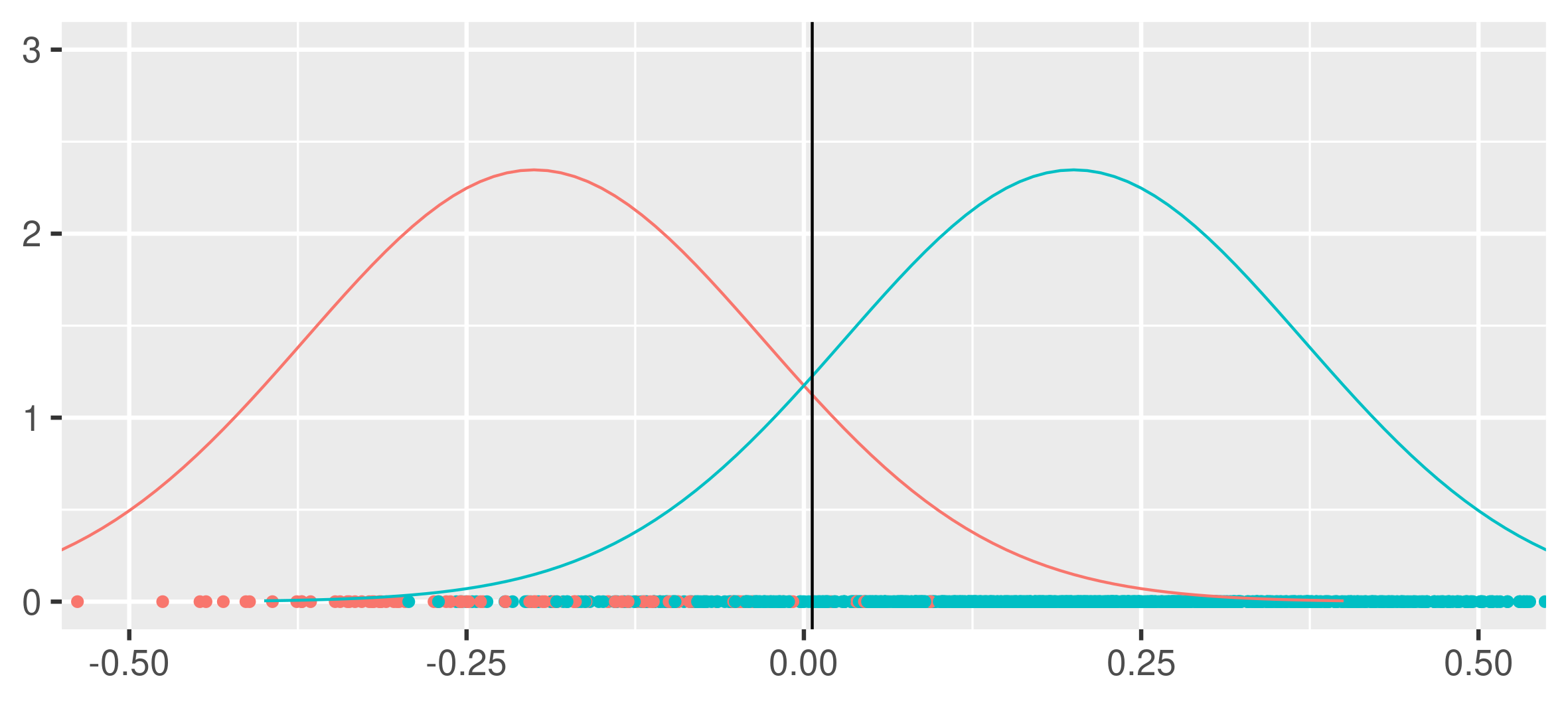
As a informal example, from [1], for undersampling, one can consider the classification problem of separating two classes \(Y\in\{0,1\}\), 100 being \(Y=0\) and 1000 being \(Y=1\). Using one feature \(X\) from the conditional distribution

\[ \begin{aligned} &X \ | \ Y=1\sim\mathcal{N}(-\mu,\sigma^2) \\ &X \ | \ Y=0\sim\mathcal{N}(\mu,\sigma^2) \end{aligned} \]

The optimal classifier is obviously \(h(x)=I(x<b^\star)\), with \(b^\star=0\). However if one applies empirical risk minimization, with \(L(x,y)=I(h(x)\neq y)\), then due to the imbalance of the dataset one is likely to choose a suboptimal classifier, due to an emphasis on classifying the majority class, as seen below.

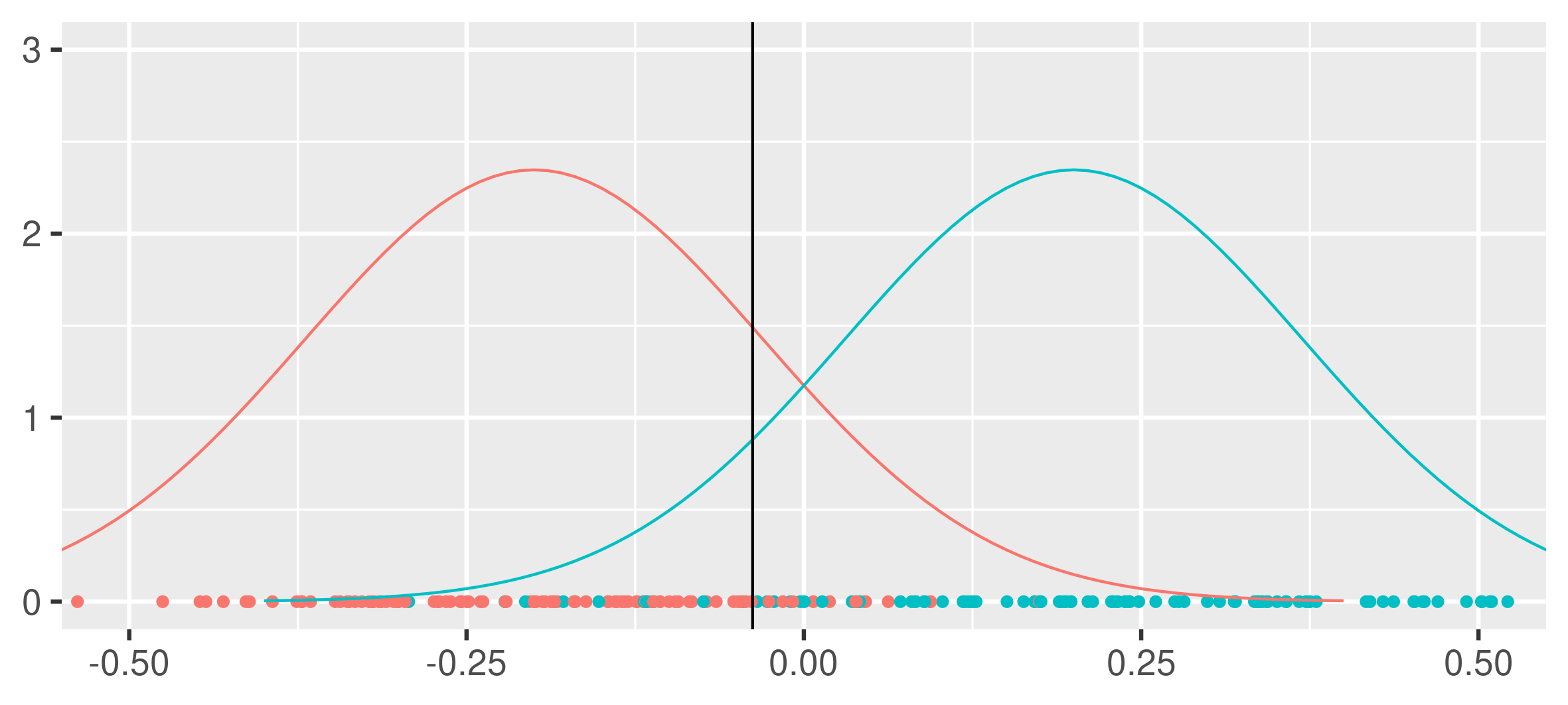
A plot of the two distributions and the generated points on the x-axis, the inferred hypothesis is the black line.

If one down-samples, s.t. both classes are equally presented, one gets a less biased but more volatile estimator.

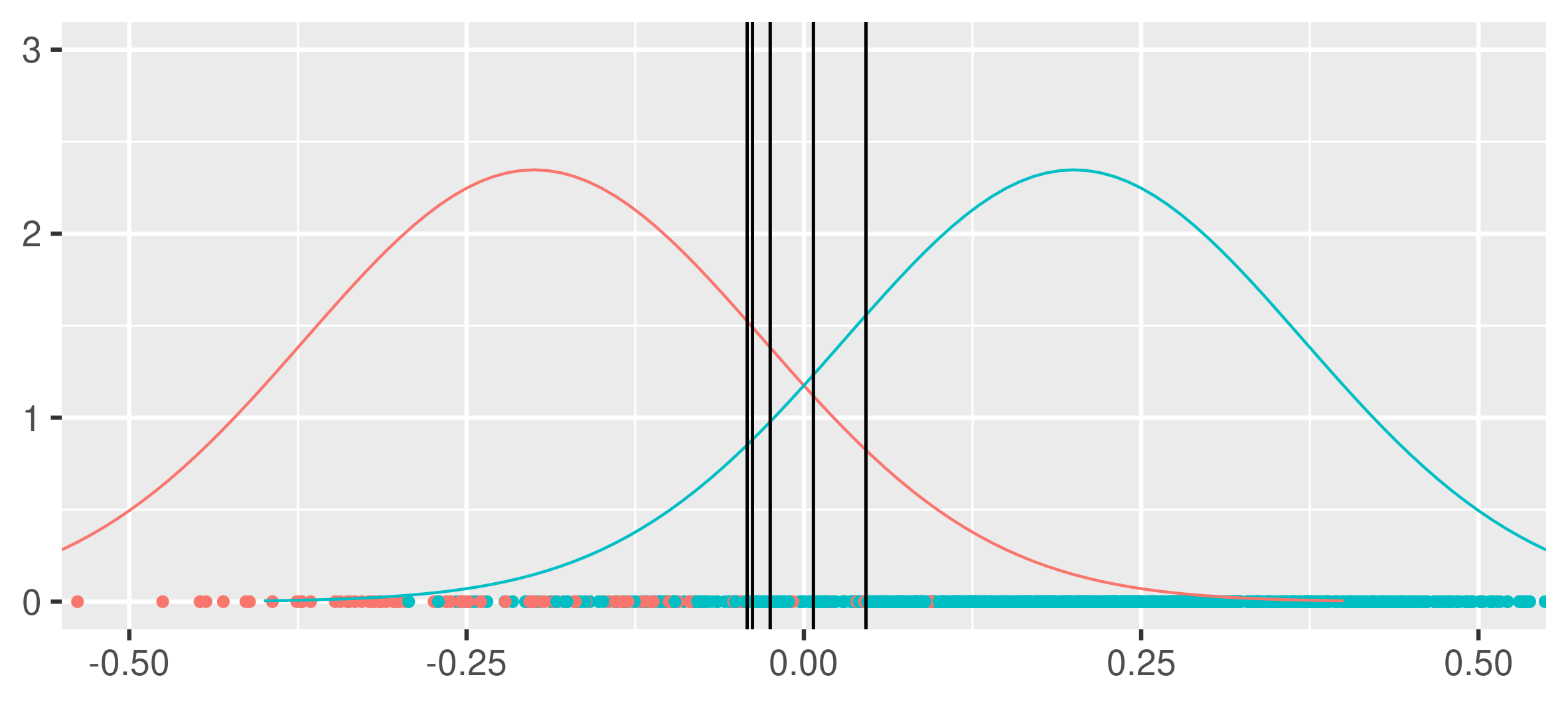
One realization of a hypothesis fitted using undersampling (top) and a multiple hypothesees fitted using undersampling (bottom).

To decrease variance, one can apply bagging as argued for in [2], i.e. sample \(B\) new bootstrap datasets and for each bootstrap dataset apply the same undersampling and fitting routine to construct a classifier, one afterwards combine the classifiers by averaging. This method is called balanced bagging or . Blagging will only be used without the bootstrap step in the thesis, i.e. taking an average of classifiers fitted using undersampling on the original dataset without the initial sampling of a bootstrap sample, this will be referred to as blagging too.

The hypothesis generated using blagging..

References

[1] Tom Fawett. Silicon Valley Data Science. 2016. https://svds.com/learning-imbalanced-classes/

[2] Byron C. Wallace and Devin Small and Carla E. Brodley and Thomas A. Trikalinos. Class Imbalance, Redux. 2011

Comments

Feel free to comment here below. A Github account is required.